论文地址
代码地址
前期调研 && blender 渲染代码
Overview
1. 这篇文章对标什么方法?
这篇文章提出的方法名为 Spin Light Uncalibrated Photometric Stereo (Spin-UP),它是一种在自然光下进行无校准光度立体摄影的无监督方法。Spin-UP对标的是现有的无校准光度立体摄影方法(NaUPS),特别是那些使用复杂的环境光模型和材料模型的方法
2. 现有方法的缺点是什么?
- 对光源和材料的强假设:许多现有方法使用简单的光模型和朗伯反射模型,这在处理具有复杂反射特性的物体时效果不佳
- 数据驱动方法的解释性差:一些基于深度学习的方法虽然在性能上有提升,但由于缺乏解释性,训练时难以约束模型,容易受到数据偏差的影响,导致对特定光源类型或反射变化敏感
- 处理一般场景能力不足:现有方法在处理自然光下的常见物体时效果有限,且在高分辨率和大量图像时难以处理
3. 这篇文章解决了什么问题?
本文提出的Spin-UP方法旨在解决以下问题:
- 提供一种新的无监督方法,在自然光下对一般物体进行光度立体摄影,无需依赖数据驱动方法的强假设和训练数据的偏差
- 通过旋转平台采集图像,减少了光的表示未知数,缓解了NaUPS问题的病态性
- 引入了可靠的光初始化方法,通过分析物体遮挡边界的像素值,减少了光与物体之间的模糊性
4. 创新点有哪些?
文章的主要创新点包括:
- 设计了一种新的NaUPS设置,通过旋转平台在静态环境光下采集图像,减少了光表示的未知数
- 提出了一个基于物体遮挡边界的光初始化方法,提高了环境光的初始化质量,减少了训练初期的模糊性
- 采用了两种训练策略:间隔采样(Interval Sampling)和缩小范围计算(Shrinking Range Computing),以降低计算成本并加快收敛速度
5. 实验结果如何?
实验结果表明,Spin-UP在综合性能上优于现有的方法:
- 在合成数据集和真实数据集上,Spin-UP在表面法线重建和环境光重建的误差度量(如平均角度误差(MAE)、PU-PSNR和PU-SSIM)上表现优越
- 对于未见过的光源,Spin-UP也展示了良好的适应性,特别是在实际应用场景中表现出较高的鲁棒性
6. 模型的输入输出是什么?
模型的输入为在不同旋转角度下采集的物体图像,输出为重建的表面法线图、环境光模型和各向同性反射率
注意:Spin-UP不恢复3D形状,只恢复观察到的表面
7. 模型结构详细介绍及实现全过程
模型结构
- 形状模型:使用神经深度场(Neural Depth Field)表示3D表面,通过多层感知器(MLP)预测深度值
- 材料模型:使用修改的Disney模型表示空间变化的各向同性反射率,包含一个预测漫反射率的MLP和一个计算镜面反射率的MLP
- 阴影模型:应用类似于之前方法的阴影掩码来处理投射阴影
实现全过程
- 图像采集:在旋转平台上采集物体的多角度图像
- 光初始化:使用边界法线和过滤器对环境光进行初始化,采用预计算的边界法线和相对旋转矩阵,通过拟合光模型参数优化环境光
- 训练策略:
- 间隔采样:通过对图像进行间隔采样,降低计算成本并确保训练的有效性
- 缩小范围计算:通过逐步缩小采样范围,提高法线计算的精度,避免局部最优
Method
3.1. Spin Light Setup 旋转光设置
数据采集设置
-
旋转平台和相机:
- 使用可旋转平台和固定相机拍摄物体。
- 平台进行360度旋转,固定角度间隔捕捉图像。
-
图像采集:
- 在旋转过程中捕获多角度的物体图像,形成图像序列 。
- 每个图像对应一个旋转角度 ,从而每个图像中光线方向 相关联。
减少未知数
-
统一光模型:
- 对所有图像使用统一的环境光模型 ,减少光表示的未知数。
- 光模型由参数化的球形高斯函数表示,每张图像只有一个1自由度的旋转角度 。
-
旋转矩阵初始化:
- 根据旋转角度 初始化旋转矩阵 ,其中 ,其余角度按照均匀分布设置 。
3.2. Light Prior from Boundaries 基于边界的光先验
整体流程
- 边界处理:提取输入图像中的边界像素 和法线 。
- 重映射:将边界像素和法线重映射到球面,并根据对应的旋转矩阵 进行旋转。
- 光探测优化:根据边界像素构成的光探测器优化 SG 光模型,得到优化后的环境光。
光初始化方法
通过优化 SG 光模型参数 来导出初始环境光模型。使用64个球形高斯(SG)基函数作为光模型,其中 。 和 分别表示高斯峰的方向、锐度和幅度。
输入:预计算的边界法线 ,初始相对旋转矩阵 ,边界像素 ,扩散过滤器 和 ,色彩过滤器 ,拟合迭代次数 ,学习率 。
输出:初始环境光模型 。
- 步骤:
- 对每个图像 ,计算边界法线 。
- 对边界像素 进行扩散过滤和色彩过滤,得到过滤后的像素值 。
- 通过最小化 优化 SG 光模型参数 。
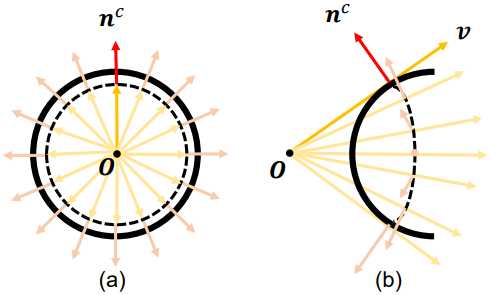
通过旋转光设置,可以利用物体边界的先验知识进行光初始化,以减轻模糊性。此方法的核心思想是观察到物体边界的像素值 提供了有关环境光的信息。对于具有遮挡边界的物体,这些边界的法线 可以预先计算出来。结合 、 和 可以粗略地导出一个光图,指示光源的位置和强度,其中 直接表示光在方向 上的强度 。但是,对于不同材料的物体,导出的光图可能包含不匹配的光源位置和色偏,导致光初始化不准确。
光源位置不匹配
光源位置不匹配是由于 中的镜面反射分量 引起的。当 占主导地位时,用 近似 是一种有偏估计,因为 是在不同方向上光的反射(见图3)。相反,当漫反射分量 占主导地位时,这种近似更为合理,因为 表示 对实际像素值的贡献最大,因此使用 表示 偏差较小。因此,为了减少光源位置不匹配的有偏估计,需要对 进行扩散过滤 。
色偏
同样,色偏是由于边界处材料的空间变化引起的。为减少色偏,需要进行色彩过滤 ,将像素值转换为灰度值。
QA
物体边界的像素值 提供环境光信息的原因
-
光与边界法线的关系:
在物体边界处,法线 通常与观察方向(摄像机视角)成直角。这意味着入射光 与边界法线之间的夹角可以直接反映在边界像素的亮度和颜色上。因此,边界像素值 可以直接用于估计环境光的方向和强度。 -
遮挡效应最小:
在物体的边界处,通常没有其他物体的遮挡,因此边界像素接收到的光线主要是来自环境光,而不是被其他物体反射或阻挡的光线。这使得边界像素的亮度和颜色信息更为纯净和直接。 -
反射特性:
在理想情况下,边界法线所代表的点的反射特性较为简单,尤其是在考虑漫反射(diffuse reflection)时,边界像素值主要反映了环境光的分布,而非复杂的多重反射或阴影效应。
为什么选择边界而不选择物体中间的部分?
-
复杂光影效果:
物体中间的部分可能受到复杂的光影效果影响,包括自阴影、反射和散射等,这些效果会使得物体中间的像素值难以直接反映环境光的真实情况。 -
多重反射和遮挡:
物体中间的像素可能会受到其他物体或自身结构的遮挡和多重反射影响,这会增加光线传播路径的复杂性,导致无法准确分离出环境光的影响。 -
计算复杂度:
在物体边界,法线方向简单明确,而在物体中间区域,由于曲面复杂多变,需要更复杂的计算来解耦光线与物体表面的相互作用。因此,选择边界像素可以简化计算过程,提高准确性。
什么叫有遮挡边界的物体?
有遮挡边界的物体是指在图像中存在明显边界的物体,这些边界的法线向量与摄像机视角成直角或接近直角。这些边界可以是物体的轮廓线或边缘,它们是光线无法透过的部分。具体而言:
-
几何遮挡:
物体的边界在几何上是光线的终止点,光线到达这里后无法继续传播,因此边界处形成了一个明显的光学和视觉上的分界线。 -
法线计算:
在这些边界处,法线向量可以通过几何方法预先计算出来,并且这些法线通常与观察方向成直角,这使得利用这些法线来估计环境光变得更加直接和准确。 -
无背景干扰:
边界像素通常不会受到背景的直接干扰,因此其光照信息更纯净,可以更好地反映环境光的实际情况。
B.1. 边界法线计算
在透视投影中,物体的边界法线计算是通过分析物体边界和视线方向之间的关系来完成的。具体来说,我们假设物体的边界在图像中呈现出遮挡效果,并且这些边界的法线与视线方向垂直。以下是具体的计算步骤:
计算步骤
-
边界法线与视线方向的关系:
在透视投影中,物体边界的法线 与视线方向 垂直,即:
其中, 是边界法线向量, 是视线方向向量。 -
边界法线与图像坐标的关系:
由于物体边界的法线与视线方向垂直,因此法线向量可以表示为:
在图像坐标系中,这意味着边界法线向量与边界像素在图像中的梯度垂直。因此,我们可以通过计算图像梯度来近似法线向量:
其中, 和 分别表示边界在x轴和y轴方向的梯度。 -
边界法线的近似计算:
在实际应用中,图像分辨率有限,物体的边界在图像中可能并不精确。为了提高计算精度,我们引入一个小的偏移量 ,用于修正法线向量:
其中,Nor表示向量归一化操作, 是一个小的常数偏移量。
示例说明
假设我们有一个物体的边界点 ,其在图像中的梯度为 和 。我们希望计算该点的法线向量 。
-
计算图像梯度:
-
计算初始法线向量:
-
修正法线向量:
3.3. Framework of Spin-UP
形状模型
使用神经深度场(Neural Depth Field)表示3D表面。使用一个多层感知器(MLP)根据图像坐标预测深度值。为了计算法线,我们扩展了[16]中描述的法线拟合方法以适应透视投影。
材料模型
我们使用修改的Disney模型表示空间变化的各向同性反射率。漫反射率 由另一个结构类似的MLP预测。空间变化的镜面反射率计算为12个球形高斯基函数的加权和,公式如下:
其中 、 和 分别表示微面法线分布、菲涅耳效应和自遮挡效应, 为视角方向, 为半角向量,计算公式为 , 为粗糙度项,初始化为 并设置为可学习参数, 为由MLP预测的权重。
阴影模型
我们应用类似于[13]的方法的阴影掩码来处理投射阴影。
损失函数
与其他基于逆向渲染的方法类似,我们使用逆向渲染损失(即公式(1))来训练框架。我们采用三阶段训练架构,并使用平滑正则项(总变差正则化)来帮助收敛,计算公式为:
其中 为图像坐标。我们在法线图 、漫反射率图 和材料的高斯基函数权重 上实施 TV(.),并按照三阶段训练架构逐渐减少它。类似于[30],我们计算归一化颜色损失 ,其中 Nor(.) 为向量归一化函数。此外,参考[16],我们计算边界损失,为预计算和估计的边界法线之间的余弦相似度。
3.4. 训练策略
优化Spin-UP需要平滑正则项来促进收敛并避免局部最优。然而,这些正则项通常在全分辨率图像上实施,导致高计算成本。为了降低计算成本和提高模型的收敛速度,我们提出了两种训练策略:间隔采样(Interval Sampling,简称IS)和缩小范围计算(Shrinking Range Computing,简称SRC)。
间隔采样(Interval Sampling)
间隔采样是一种从图像中采样光线的策略,用于降低计算成本。与随机采样或基于块的采样不同,间隔采样可以保持物体的形状。具体操作如下:
-
图像分块:
首先,将全分辨率的图像划分成若干个不重叠的块,每个块包含 个像素点。 -
像素点提取:
从每个块中提取相同位置的像素点(例如,每个块的左上角像素),得到若干个分辨率较低的子图像。 -
子图像采样:
在训练过程中,这些子图像会在每个训练周期内随机采样。平滑正则项(例如总变差正则化)基于子图像的分辨率进行计算,这样既降低了计算成本,又确保了平滑正则项的有效性。
通过间隔采样,训练时间减少了一半(例如从每个物体平均60分钟减少到25分钟),同时GPU内存占用也降低了五倍(从25 GB减少到5 GB)。
缩小范围计算(Shrinking Range Computing)
缩小范围计算是一种用于在间隔采样过程中避免混叠(aliasing)问题的策略。由于在子图像分辨率下计算法线时需要四个相邻点的深度,可能会导致计算精度下降。为了解决这个问题,我们采用缩小范围计算策略:
-
使用全分辨率相邻点:
在子图像的每个像素进行法线计算时,使用全分辨率图像坐标系中相邻的四个点的深度值,而不是子图像中的相邻点。 -
逐步缩小范围:
在训练的早期阶段,选择距离查询点较远的相邻点(例如距离3个像素)进行法线计算,这样可以得到更平滑和稳定的法线图,有助于避免局部最优。在训练的后期,逐步选择距离查询点较近的相邻点,最终提高法线计算的精度。
为什么IS和SRC能提升性能
间隔采样(IS)
-
降低计算成本:
将全分辨率图像划分为多个低分辨率子图像,减少了每次训练迭代中需要处理的数据量。这样大大降低了计算成本和所需的GPU内存,从而加快了训练速度。 -
保持全局形状信息:
不同于随机采样或块采样,间隔采样能够保留物体的整体形状特征。这意味着在训练过程中,模型可以学习到更加全面的物体信息,避免因采样不均匀而丢失重要的结构信息。 -
有效的正则化:
通过在低分辨率子图像上计算平滑正则项(如总变差正则化),确保了这些正则项在训练过程中的有效性。同时,计算成本的降低使得可以在更多的迭代中应用正则化,进一步提高模型的泛化能力。
缩小范围计算(SRC)
-
提高法线计算的精度:
在子图像上直接计算法线时,由于分辨率降低,可能会导致法线计算不准确。缩小范围计算通过使用全分辨率图像坐标系中的相邻点来计算法线,确保了法线计算的精度。这有助于模型更准确地学习物体的几何信息。 -
避免局部最优:
在训练的早期阶段,使用距离查询点较远的相邻点进行法线计算,可以获得更加平滑和稳定的法线图。这种平滑的法线图有助于模型避免陷入局部最优解,从而提高全局收敛性。 -
逐步精细化:
在训练的后期,逐步缩小选择的相邻点范围,从较远的点逐渐过渡到较近的点,使得法线计算更加精细。这种逐步精细化的过程可以在保证初期全局收敛的基础上,进一步提升后期的局部精度,从而提高模型的整体性能。
透视投影下的法线计算
为了在透视投影下计算法线,我们扩展了[16]中描述的法线拟合方法。这个方法通过多层感知器(MLP)预测物体表面的深度值,然后通过这些深度值计算每个像素的法线。
具体步骤
-
深度值预测:
使用 MLP 根据图像中的每个像素的二维坐标预测深度值 。得到一个深度图 。 -
相邻点的选择:
对于每个像素 ,选择其周围的四个相邻点 ,这些点的深度值分别为 。 -
转换到相机坐标系:
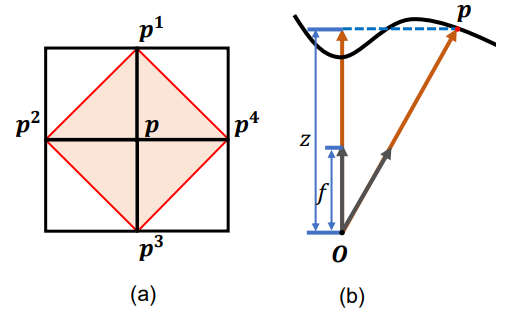
将这些像素点从图像坐标系转换到相机坐标系。转换公式为:
其中 , 是相机的焦距, 和 分别是相机帧的宽度和高度的一半。 -
法线计算:
根据相邻点计算当前像素点的法线。法线 可以通过以下公式计算:
其中 。
下面详细解释每个部分:
-
法线向量 :
法线向量 是一个单位向量,表示表面在当前点的方向。 -
相邻点和当前点:
- :当前像素点的位置。
- :第 个相邻像素点的位置。
- :当前像素点的投影位置。
- :第 个相邻像素点的投影位置。
-
深度值:
- :当前像素点的深度值。
- :第 个相邻像素点的深度值。
-
深度差值 :
用于表示相邻点的深度差值:
这反映了相邻点与当前点之间的深度变化情况。
-
向量长度 :
是深度差值 的绝对值,表示深度变化的程度。 -
叉积 :
- 和 是两个相邻像素点与当前像素点之间的位移向量。
- 叉积 计算的是这两个向量的法向量,即垂直于这两个向量的向量。
-
加权平均:
法线向量 是通过对每个相邻点的法向量进行加权平均得到的,权重是深度差值的绝对值 。 -
归一化:
最后,法线向量 被归一化,使其成为单位向量,即其长度为1。这通过除以所有权重的总和 实现。
综合以上解释,公式的含义是:通过计算相邻点与当前点之间的深度差值和位置差异来估计当前像素点的法线向量。公式考虑了深度变化的程度,并对相邻点的法线向量进行加权平均,从而得到一个准确的法线估计。
全流程
数据采集
-
设置旋转平台和相机:
- 准备一个可旋转的平台和固定的相机。
- 将待拍摄的物体放置在平台中央,并确保相机对准物体。
-
旋转拍摄:
- 启动平台旋转,通常进行360度旋转。
- 在旋转过程中,以固定角度间隔(例如每旋转2度)捕捉物体的图像,最终获得一组多角度图像。
-
图像处理:
- 对每个捕捉到的图像进行预处理,如去除噪声和校正颜色。
- 确定每个图像中物体的边界,生成掩码以便后续处理。
数据预处理
-
深度图预测:
- 使用多层感知器(MLP)根据每个像素的二维图像坐标预测其深度值,生成深度图 。
-
边界法线计算:
- 根据物体在图像中的边界,计算每个边界像素的梯度 和 。
- 使用梯度计算初始法线向量 。
- 引入小偏移量 ,修正法线向量 ,其中Nor表示向量归一化。
渲染方程中的法线计算
-
选择相邻点:
- 对于每个像素 ,选择其周围的四个相邻点 ,这些点的深度值分别为 。
-
转换到相机坐标系:
- 将这些像素点从图像坐标系转换到相机坐标系:
其中 , 是相机的焦距, 和 分别是相机帧宽度和高度的一半。
- 将这些像素点从图像坐标系转换到相机坐标系:
-
法线计算:
- 使用下式计算法线:
其中 。
- 使用下式计算法线:
光初始化
-
边界处理:
- 提取输入图像中的边界像素 和法线 。
-
重映射:
- 将边界像素和法线重映射到球面,并根据对应的旋转矩阵 进行旋转。
-
光探测优化:
- 根据边界像素构成的光探测器优化 SG 光模型,得到优化后的环境光。
训练策略
-
间隔采样(IS):
- 将全分辨率图像划分为不重叠的块,每个块包含 像素点。
- 从每个块中提取相同位置的像素点,生成低分辨率子图像。
- 在训练过程中,这些子图像在每个周期内随机采样,平滑正则项基于子图像的分辨率进行计算。
-
缩小范围计算(SRC):
- 在子图像分辨率下,使用全分辨率图像坐标系中的相邻点进行法线计算。
- 在训练的早期阶段,选择距离查询点较远的相邻点进行法线计算,以获得更平滑和稳定的法线图。
- 在训练的后期,逐步选择距离查询点较近的相邻点,最终提高法线计算的精度。
最终法线图生成
-
法线图优化:
- 使用优化后的法线和环境光模型,通过迭代优化,生成最终的法线图。
-
法线图输出:
- 输出生成的法线图,用于进一步的3D重建和渲染。
Related Work
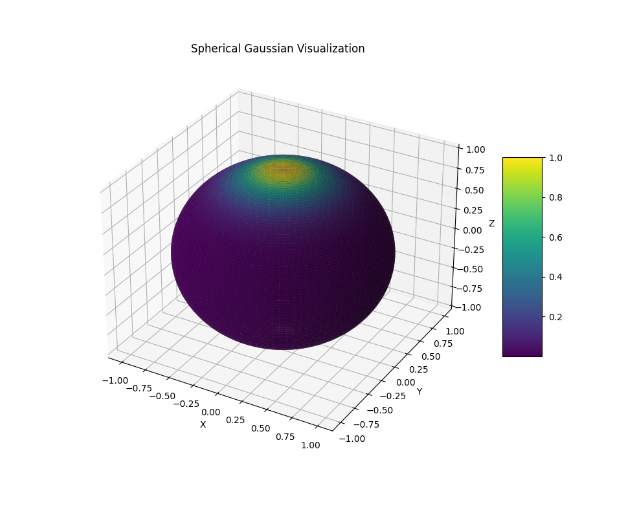
球面高斯函数 SG
其中:
- 是波瓣的方向,即高斯函数的中心点。
- 控制波瓣的锐度,类似于平面高斯函数中的参数 。
- 是波瓣的幅度或强度。
测试用代码:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 定义球面高斯函数
def spherical_gaussian(dir, mu, sharpness, amplitude):
cos_angle = np.dot(dir, mu)
return amplitude * np.exp(sharpness * (cos_angle - 1.0))
# 生成球面上的点
def generate_sphere_points(num_points=100):
phi = np.linspace(0, np.pi, num_points)
theta = np.linspace(0, 2 * np.pi, num_points)
phi, theta = np.meshgrid(phi, theta)
x = np.sin(phi) * np.cos(theta)
y = np.sin(phi) * np.sin(theta)
z = np.cos(phi)
return x, y, z, phi, theta
# 可视化球面高斯函数
def plot_spherical_gaussian(mu, sharpness, amplitude):
x, y, z, phi, theta = generate_sphere_points()
sg_values = np.zeros_like(x)
for i in range(x.shape[0]):
for j in range(x.shape[1]):
dir = np.array([x[i, j], y[i, j], z[i, j]])
dir = dir / np.linalg.norm(dir) # 归一化方向向量
sg_values[i, j] = spherical_gaussian(dir, mu, sharpness, amplitude)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 使用面图表示SG值
ax.plot_surface(x, y, z, facecolors=plt.cm.viridis(sg_values), rstride=1, cstride=1, alpha=0.9, linewidth=0)
m = plt.cm.ScalarMappable(cmap=plt.cm.viridis)
m.set_array(sg_values)
# 在指定的 Axes 对象上添加颜色条
fig.colorbar(m, ax=ax, shrink=0.5, aspect=5)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Spherical Gaussian Visualization')
plt.show()
# 设置SG参数
mu = np.array([0, 0, 1]) # 波瓣方向
sharpness = 10.0 # 波瓣锐度
amplitude = 1.0 # 波瓣幅度
# 可视化球面高斯函数
plot_spherical_gaussian(mu, sharpness, amplitude)
球谐函数和球面高斯函数
球谐函数(Spherical Harmonics, SH)
定义和特性:
- 数学定义:球谐函数是一组正交函数,定义在球面上,可以用于表示球面上的任意函数。它们类似于傅里叶级数,但用于球面上的函数分解。
- 频域表示:球谐函数通常用于频域表示,可以有效地表示低频信号。对于高频信号,球谐函数需要较高阶数的分解,且表示会变得模糊。
- 用途:在计算机图形学中,球谐函数广泛用于近似间接光照(如环境光遮蔽和全局光照)和漫反射光照,因为它们可以高效地表示和处理光照的漫反射部分。
- 优点:球谐函数可以有效地处理复杂的光照分布,计算效率高,适合实时应用。适用于表示低频光照信息。
- 局限性:高频信号会导致球谐函数表示模糊,不适合表示镜面反射等高频细节。
球面高斯函数(Spherical Gaussians, SG)
定义和特性:
- 数学定义:球面高斯函数是一种基于高斯函数的球面上的函数,通常用于表示方向上的分布。SG可以视为在球面上的高斯分布,具有方向性和集中性。
- 空间域表示:球面高斯函数在空间域中具有较强的方向性,可以表示高频和集中分布的信号,适合表示光照中的高光和镜面反射部分。
- 用途:在计算机图形学中,球面高斯函数用于预计算光照中的镜面反射,适合表示方向性强的高光部分。也用于环境光照的预过滤和实时反射。
- 优点:能够精确表示高频细节,适合处理镜面反射和高光效果。计算过程中可以直接使用高斯函数的性质,进行高效的卷积计算。
- 局限性:在处理广域漫反射光照时,球面高斯函数不如球谐函数有效。
联系和区别
联系:
- 用途重叠:两者都用于预计算光照和实时光照计算,但通常分别应用于不同类型的光照(漫反射 vs 镜面反射)。
- 组合使用:在实际应用中,球谐函数和球面高斯函数可以结合使用。例如,球谐函数用于表示漫反射光照,而球面高斯函数用于表示镜面反射光照,这样可以同时处理场景中的低频和高频光照信息。
区别:
- 频域 vs 空间域:球谐函数适用于频域表示,特别是低频信号,而球面高斯函数更适用于空间域表示,特别是高频信号。
- 适用范围:球谐函数主要用于间接光照和漫反射,球面高斯函数主要用于直接光照和镜面反射。
- 表示能力:球谐函数在高频信号表示上存在模糊问题,而球面高斯函数可以精确表示高频信号。
总的来说,球谐函数和球面高斯函数是两种互补的工具,在计算机图形学中结合使用,可以更全面地处理不同类型的光照效果,提供更加逼真的渲染结果。

