概率为 0 的事件与任意事件相互独立
全概率公式做题步骤
- 确定要求的事件A
- 找完备事件组,列出各种情况Bi(i=1,2,3...)
- 在情况Bi下,事件A发生的概率,P(A) = ∑P(Bi)P(A|Bi) = ∑P(ABi)
注意,事件A零碎分布于事件B,所以需要将B的各种情况合起来计算
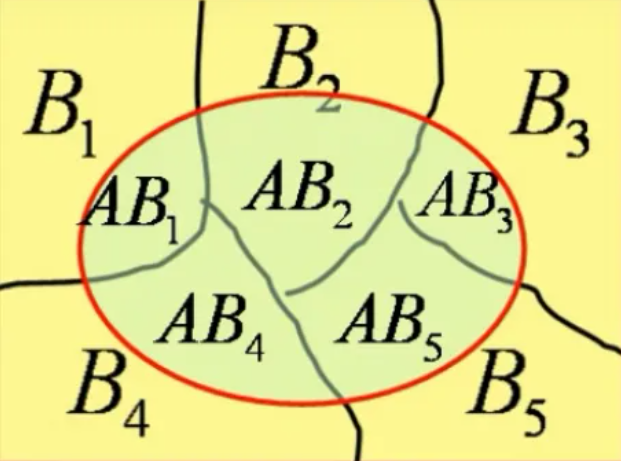
将自然语言和数学语言相互转化,找到对应的值
分布函数
分布函数端点值的辨析:
理解分布函数(概率论)
注意
只有连续型分布有分布函数和概率密度,离散型没有
混合型概率分布只有分布函数,没有概率密度
分布函数连续 ⇔ 连续型随机变量
分布函数必须右连续,只是针对点而言,右连续的函数也可以不是连续函数
联合概率
注意,已知边缘分布,不能推得联合分布,当且仅当边缘分布相互独立的时候,可以通过相乘来确定联合分布
用联合概率密度求 Z(x,y)
当作二重积分算,积分区域是 xy 的范围,被积函数是 f(x,y),要移动的图像是 P{} 内的函数
比如 P{X+Y>1} ,选定一个要积的变量,比如x,则 y>1-x
作图,在积分区域里积分,得到概率值。
🔺注意:不管积分区域是什么样,也就是 P{} 括号内的函数是什么样,和联合分布函数无关。联合分布函数都是 f(x, y) (被积函数)
求 z = g(x, y) 的分布函数
- xy都是离散型,很简单,直接看就行
- xy都是连续型,则把 z 看作常数,讨论 z 的范围,然后再用上面联合概率密度求概率的方法
- x是离散型,y是连续型(离连型)全概率公式+分布函数法
先写出 P{ X + Y ≤ Z } ,然后用全概率公式,分为 P{ X + Y ≤ Z ,X=0} P{ X + Y ≤ Z ,X=1} 等区间
然后带入 X=0,X=1,化简表达式,变成 P{ X=0,Y ≤ Z },P{ X=1,Y ≤ Z-1 }
然后讨论 z 的范围,根据 X+Y=Z 来估计。比如 0<X<1,0<Y<1,那么 讨论 Z ∈(0,2)比如 z<0 时,Fz(z)=0
当 z 的取值在积分区域里时,用二重积分计算概率值
关于概率论里的Z=max{X,Y},min{ X,Y }分布的理解与计算方法
数字特征
连续型求期望
先求密度:先用 P{U≤u} 卡出分布函数,然后求导
判断相关和独立
X Y 不相关 ⇔ EXY = EXEY (ρ=0)
X Y 独立 ⇔ FXY = FXFY 或者 f(xy) = f(x)f(y)

