NeRF，即 Neural Radiance Fields（神经辐射场）
Title：NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
将场景表示为用于视图合成的神经辐射场

官网
NeRF-pytorch

入门讲解
十分钟带你快速入门NeRF原理
【较真系列】讲人话-NeRF全解（原理+代码+公式）

参考博客
NeRF入门之体渲染 (Volume Rendering)
【三维重建】NeRF原理+代码讲解

输入：不同位姿相机拍摄的物体图片&相机参数（位姿、内参）
输出：新视角下的物体图片

不成形的思考

流程
拍摄不同位姿的图片，获得多视角的物体图像
每个相机的位置（xyz）和位姿，也就是朝向（用θ和φ表示），作为输入
每个图片上的每个像素对应一个射线，这条射线贯穿图片像素和实际物体上的一个点
在射线上均匀取一些采样点（sample_points）作为评估，每个点都输出颜色和密度
使用体渲染技术，对这些点的颜色和密度进行积分，合成一个像素颜色
将这个颜色和真实颜色做MSE，来训练网络

Q
有监督学习？标签是什么

理论角度
体渲染：对烟雾、胶体等非不透明刚体组成的物体进行渲染，对光路上的发光点进行积分（下面步骤是基于这个理念）
NeRF假设物体是这样一些微小粒子组成的，且这些粒子是自发光的（后续有用）

具体步骤，每个像素点和每个实体点之间连一条射线
这个射线代表从物体某些在同一直线上的自发光点发出的光线，射在对应视角图片中的一个像素点上
（射线如何确定？通过相机的位置和像素点的位置来确定的。具体来说，从相机的焦点出发，通过每个像素点构建一条射线。这些射线穿过场景并捕获沿途的光照信息。）
在射线上均匀采样一些点，假设是由这些点发光而成的光线（为什么这样采样？为了在射线上获得代表性的点，这些点可以近似射线经过的场景。均匀采样有助于模型学习不同深度处物体的光照和颜色特性，使得重建的场景更为精确和连续。）采样点位置 r(t) 计算：r(t)=o+td o：起点坐标，相机所在位置 t：采样点距离 d：单位向量
为了舍去双边缘效应，进行重采样（详细描述。减少边缘模糊或阴影错误。在初步的均匀采样后，根据初步估计的体密度（density），对那些可能对最终颜色贡献更大的区域进行更密集的采样。这种策略可以更精细地捕捉到细节和边缘。）
然后利用体渲染公式，将每个像素点-射线对上的采样点进行积分，计算出每个像素点的density和RGB值
（如何计算的？）
利用得到的像素值和真实图片的像素值作损失，自监督学习，来训练网络

网络结构
输入采样好的像素-光线对（如何选择batchsize？）和相机内参
用这些计算出光线的参数，获得一个5D坐标（如何计算？）
8层MLP，用ReLU函数
得到 RGBσ 4D坐标
体渲染→计算像素值→计算损失、优化网络
将模型信息隐式的保存在网络中
再输入一张图片就可以得到该视角下的 RGBσ 信息，渲染为一张图片（如何渲染？）

体渲染技术：模拟了光线在非均匀介质中的传播
它的目的主要是为了解决云、烟、果冻这类非刚性物体的渲染建模，可以简单理解为是为了处理密度较小的非固体的渲染。当然进一步推广到固体的渲染也说的通，当密度逐渐增大，近似为一个不透明的固体

What's new?

Insight

以往：直接通过图片重建出一个网格/点云/体素的模型
NeRF：神经隐式的方式重建三维模型（implicit representation）

显示：有明确xyz的信息，mesh、体素、点云
隐式：用神经网络来表示三维空间中的场景属性（如颜色、密度等）的方法，而不是使用传统的显式几何结构（如点云、多边形网格等）

这种隐式表示的优势在于它可以非常精细地捕捉场景的细节，而不需要存储大量的几何数据。由于神经网络可以表示非常复杂的函数，这种方法可以用来重建具有高度细节和复杂几何结构的场景。
在NERF中，隐式表示允许我们通过简单的函数查询来渲染高质量的图像，而不需要知道场景的确切几何形状。这使得NERF非常适合于基于图像的三维重建任务，因为它可以处理大量的输入图像，并且能够生成连贯的三维场景表示。

Method

1. 5D neural radiance fields 5D神经辐射场
2. classical volume rendering techniques 经典体渲染技术
3. position encoding to map each input 5D coordinate into a higher dimensional space 使用位置编码将5D坐标映射到高维空间

输入：5D的相机位姿，输出：4D向量：RGB和不透明度α（密度）
模型结构：8层MLP
2D图片→5D向量→NeRF→4D向量→2D图片

2D图片上的一个像素点为3D空间中一条射线上点之和（一个像素对应一条射线）
利用相机模型反推射线，射线表示为 r(t)=o+td

在一定范围内，取一组采样点（用near和far表示光线最近点和最远点）每个采样点都有RGBA的值
射线方向上对采样点进行积分得到像素点确切的颜色值
所以NeRF渲染的是一个个点，像雾状的东西，称为体积雾

经典体渲染技术
位置 x =（x, y, z）
体积密度 σ(x) 可以解释为光线在位置 x 处终止于一个无限小粒子的微分概率。
相机光线 r(t)=o+td 的预期颜色 C(r)，其中 tn 和 tf 是近和远的边界
T(t) 表示从 tn 到 t 沿光线的累积透射率，即光线从 tn 到 t 行进而不撞击任何其他粒子的概率

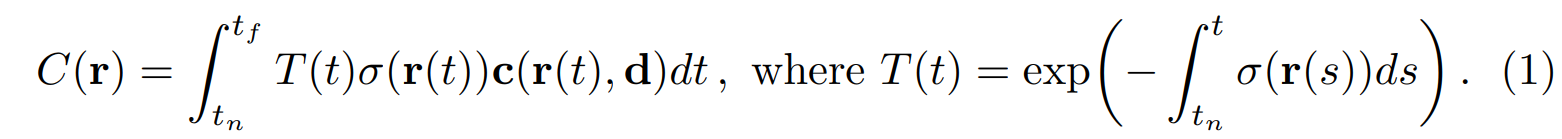
位置编码
采用位置编码提高图片细节质量，将图片中的高频信息体现出来

将图像的像素坐标映射为相机坐标系，再从相机坐标系映射为世界坐标系下的一些点
将点输入到NeRF网络中，得到该点的RGB值和不透明度（密度）
根据体渲染公式，将点映射回像素值，称为预测值
将预测值和真实值做一个损失，可以优化网络的运行

NeRF假设
物体是自发光的粒子、粒子本身有密度和颜色

将物体进行稀疏表示的单个粒子的位姿，输出的是粒子的密度和颜色

一个点对应一个相机位姿是一个训练数据单位，而不是以图片为单位

NeRF的优势

NeRF（Neural Radiance Fields）提供了若干相对于以前视图合成和三维重建模型的显著优势。这些优势主要包括：

1. 连续的场景表示

• 细节与连续性：NeRF表示场景为一个连续的、高度详细的函数，允许从任何视角生成非常平滑和连续的视图。这与传统的基于离散三维网格（如体素网格）或多边形网格的方法相比，可以生成更自然的过渡和更精细的细节。

2. 处理复杂光照和材料

• 视角依赖效果：NeRF能够捕捉复杂的光照效果，如高光和阴影，以及非朗伯特（非漫反射）表面的视角依赖特性，这些在传统方法中往往难以准确渲染。

3. 高质量的新视角合成

• 逼真度：NeRF通过优化整个场景的辐射场来重建新视角，生成的图像在视觉上与真实世界的观察极为接近，特别是在合成高度逼真视图方面的表现优于许多先前技术。

4. 更少的先验几何需求

• 自底向上的学习：与需要明确的3D模型或复杂场景几何先验的方法不同，NeRF仅依赖于输入的二维图像和相应的相机参数来学习场景的3D表示，不需要复杂的场景建模步骤。

5. 可微分渲染

• 端到端优化：NeRF使用可微分的体积渲染技术，这使得可以通过标准的梯度下降技术直接从图像误差中优化网络参数，实现端到端的训练。

6. 存储和计算效率

• 参数化表示：虽然NeRF需要大量的计算资源进行训练和渲染，但它将整个3D场景以及相关的视角依赖特性编码在一个相对紧凑的神经网络中，这比传统的大规模3D数据结构更加存储高效。

挑战与局限

尽管NeRF有诸多优势，但它也存在一些局限，如渲染速度慢（因为需要大量的网络评估来渲染每个视图）和训练成本高。此外，对于动态场景的处理也是NeRF目前的一个挑战点，尽管已有研究在尝试解决这些问题。

总的来说，NeRF在视图合成和三维场景重建领域提供了一种创新的方法，通过其连续的、高度详细的场景表示能力，以及对复杂光照和材料特性的处理，显著提升了渲染的真实感和质量。

Relative Works

表示方式
3D重建几种表现形式——深度图，体素，点云，网格

三角形网格（triangle mesh）是最常用的表示形式。这主要是因为三角形具有以下优点：

1. 稳定性：三角形是唯一一种在任何情况下都不会变形的多边形，这意味着它们可以很好地适应复杂的形状而不失去稳定性。
2. 一致性：由于所有的三角形都有三个顶点和三个内角，因此它们在计算和渲染时具有一致性，这使得算法的实现更加简单和高效。
3. 灵活性：三角形可以组合成几乎任何形状，从简单的几何体到高度复杂的有机形状，都可以通过三角形网格来近似表示。
4. 渲染优化：现代图形硬件和渲染管线针对三角形渲染进行了优化，因此使用三角形网格可以充分利用这些优化，提高渲染效率。
5. 易于处理：在许多图形处理任务中，如碰撞检测、光线追踪和阴影计算，三角形网格比其他类型的多边形网格更容易处理。
   尽管四边形网格（quadrilateral meshes）在某些情况下也有其优势，例如在需要平滑曲面的应用中，但三角形网格的通用性和易用性使得它们在大多数情况下成为首选。在实际应用中，即使是四边形网格也常常被分解成三角形来进行渲染和处理。

几种坐标系
相机模型、参数和各个坐标系(世界坐标系、相机坐标系、归一化坐标系、图像坐标系、像素坐标系之间变换）
在三维重建过程中，通常会涉及多种坐标系，主要包括以下几种：

1. 世界坐标系（World Coordinate System）：
   • 世界坐标系是一个固定的坐标系，用于描述场景中物体和相机的绝对位置。
   • 它是一个三维直角坐标系，通常定义在场景的某个方便的位置和方向上。
   • 世界坐标系是进行三维重建时的参考框架，所有的物体和相机的位置都是相对于这个世界坐标系来描述的。
2. 相机坐标系（Camera Coordinate System）：
   • 相机坐标系是以相机的光心为原点的三维直角坐标系。
   • 在这个坐标系中，X轴通常水平向右，Y轴垂直向上，Z轴与光轴重合，指向相机前方。
   • 相机的内参和外参参数用于将世界坐标系中的点转换到相机坐标系中。
3. 图像坐标系（Image Coordinate System）：
   • 图像坐标系是二维坐标系，用于描述成像平面上的点。
   • 它通常以图像的左上角为原点，X轴向右，Y轴向下。
   • 图像坐标系中的坐标单位通常是像素。
4. 归一化图像坐标系（Normalized Image Coordinate System）：
   • 归一化图像坐标系是图像坐标系的一种变换形式，其中每个点的坐标都除以该点的Z坐标（即相机坐标系中的深度值）。
   • 在归一化图像坐标系中，成像平面的中心通常位于坐标原点，X轴和Y轴的范围通常是[-1, 1]。
5. 像素坐标系（Pixel Coordinate System）：
   • 像素坐标系是图像坐标系的一种特殊形式，其中坐标的原点通常位于图像的左上角，X轴向右，Y轴向下。
   • 像素坐标系的单位是像素，它直接对应于数字图像中的阵列结构。
     在进行三维重建时，通常需要将这些不同的坐标系相互转换，以便从二维图像中恢复出三维信息。例如，通过相机标定可以得到相机内参，将图像坐标系中的点转换到归一化图像坐标系，然后再通过相机外参将归一化图像坐标系中的点转换到世界坐标系中进行三维重建。

相机标定
三维重建第三课：相机标定原理步骤(一）坐标系变换
相机标定的基本原理与经验分享
世界坐标系到相机坐标系：先旋转（R）再平移（T）

思考

对于变量A和结果R，如何发现两者是否有映射关系？
本文中5D向量输入，4D的RGB+density输出，这个映射关系看似很难以想到，但是它来自于一个传统的体渲染思路。本文仅使用MLP将其转化为CV领域，便是一种创新。

对于一种想达到的结果R，一个变量组A在映射F下得到的R效果不好，而另一组变量B在映射F下得到的R效果要好，这就是科研中创新的过程

如何发现映射关系？站在巨人肩膀上，将其他领域应用于本领域；感性认知，加上手动验证，比如用ML方法验证，然后再投入实验。

英文单词

state-of-the-art：最先进的
sparse：稀疏的
optimize：优化
spatial：空间的
rendering：渲染
continuous：连续的
map：映射
coordinate：坐标
world coordinate：世界坐标系
synthesize：合成
differentiable：可微的
density：密度（不透明度）
geometry：几何
outperform：比...做的好
referred to：被称为
corresponding：相对应的
pipeline：流程、框架
voxel grids：体素网格
infinitesimal：无穷小
particle：粒子
triangle meshes：三角网格