时序模型

t 时刻的状态和前面的数据相关
自回归：预测（同一序列）后面的值，是根据（同一序列）前面的值来预测，即使用自身过去数据预测未来

潜变量模型

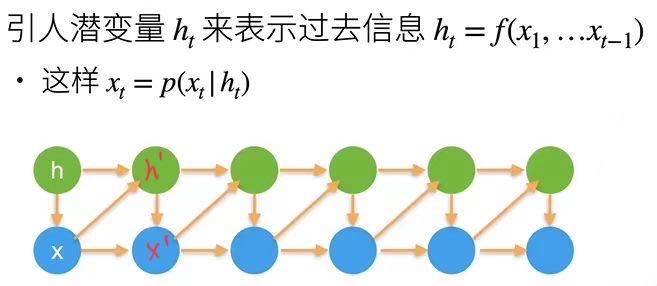
h' 包含了 h 和 x 的信息，也就是之前状态的信息

马尔可夫模型

马尔可夫性质：系统的下一个状态只依赖于当前状态，而与之前的状态无关。具有“无记忆性”

马尔可夫假设：第N个词的出现只与前面N-1个词相关，而与其它任何词都不相关。N-gram模型就是基于该假设构建的

马尔科夫链

是依赖于马尔可夫假设的最基本的模型，用于模拟随即系统的状态转移
未来的状态只取决于现在的状态，和之前的步骤无关
任何状态所有出箭头概率之和为1
转移状态矩阵：类似于有向图
要找到在 n 步转移中，由状态 i 转移到状态 j 的概率，只需要找到 n 阶状态转移矩阵第 i 行 j 列

隐马尔可夫模型 HMM

HMM 在马尔可夫链的基础上增加了“隐状态”和“观测状态”的概念。HMM 在马尔可夫链的基础上加入了观测数据，用于处理观测与状态间存在某种隐含关系的情况。

在 HMM 中，系统的真实状态（隐状态）不能直接观测，只能通过一些观测到的事件（观测状态）间接推断。

HMM 被广泛应用于序列数据的建模，如语音识别、生物序列分析等，其中系统的内部状态不是直接可见的。

隐马尔可夫模型（Hidden Markov Model, HMM）是一种统计模型，它用于描述一个观测序列背后的一个不可观测（隐含）状态序列。这个模型假设隐含状态生成观测数据的过程具有马尔可夫性质，即每个状态的发生仅依赖于它之前的一个状态。隐马尔可夫模型在语音识别、自然语言处理、生物信息学和其他许多领域有广泛的应用。

隐马尔可夫模型主要包含以下几个组成部分：

隐状态集合：模型中不可直接观测到的内部状态的集合。
观测集合：每个隐状态可以生成的观测数据的集合。
状态转移概率矩阵：隐状态之间转移的概率，表示为一个矩阵。矩阵的每个元素 aij 表示从状态 i 转移到状态 j 的概率。
观测概率分布：也称为发射概率，它表示在给定某个隐状态的情况下，生成某个观测值的概率。
初始状态概率分布：模型在开始时每个隐状态的初始概率分布。

隐马尔可夫模型的基本假设包括：

马尔可夫假设：每个隐状态仅依赖于它之前的一个隐状态。
观测独立性假设：任何时刻的观测值仅依赖于当前的隐状态，与其他隐状态或观测值无关。

隐马尔可夫模型的三个基本问题：

评估问题：给定模型参数和观测序列，计算观测序列出现的概率。这通常通过前向算法或后向算法解决。
解码问题：给定模型参数和观测序列，找出最有可能产生这些观测的隐状态序列。这通常通过Viterbi算法解决。
学习问题：给定观测序列，估计模型参数（状态转移概率、观测概率和初始状态概率），使得观测序列的概率最大。这可以通过Baum-Welch算法（一种特殊的期望最大化算法）来解决。

马尔可夫决策过程

马尔可夫决策过程（Markov Decision Process, MDP）是一种数学框架，用于形式化描述在不确定性环境中的决策制定问题。MDP 适用于那些决策结果部分依赖于决策者并且部分依赖于随机因素的情形。MDP 主要用于需要做出一系列决策的场景，如自动控制、经济学决策、强化学习等，目标是找到最优策略，以最大化长期奖励。

MDP 在马尔可夫链的基础上加入了“决策”的元素，引入了动作（Actions）、状态转移概率和奖励（Reward）。不仅关注状态的转移，还关注在给定状态下采取不同动作所导致的后果和收益。

一个 MDP 主要由以下四个元素组成：

状态（S）：描述决策过程中可能到达的所有状态的集合。每个状态提供了决策环境的完整描述。
动作（A）：对于每个状态，都有一组可能的动作（或决策）。动作决定了状态转移的可能性。
状态转移概率（P）：表示为 P(s'|s, a)，即在状态 s 下采取动作 a 后转移到状态 s' 的概率。这个概率捕捉了环境的动态性和不确定性。
奖励（R）：函数 R(s, a, s') 表示从状态 s 采取动作 a 并转移到状态 s' 所得到的即时奖励（或成本）。奖励函数评估每个动作的即时效用。

目标是找到一个策略（Policy），即从每个状态到动作的映射，以最大化某种性能标准，通常是预期收益的总和。这种性能标准可以是累积奖励的总和，也可能涉及对未来奖励的贴现（Discounting）。

在解决 MDP 问题时，通常涉及到两种主要的策略：

价值迭代（Value Iteration）：通过不断迭代更新状态值函数来逼近最优解，直到达到稳定状态。
策略迭代（Policy Iteration）：包含两个步骤，策略评估（计算当前策略的值）和策略改进（基于当前值函数更新策略），这两个步骤交替进行直到策略收敛。

MDP 提供了一种强大的框架来模拟和解决决策问题，尤其是在考虑时间和不确定性时。在强化学习中，智能体通过与环境的交互来学习最优策略，通常是在没有初始知识的情况下通过试错学习。

马尔可夫随机场

马尔可夫随机场（Markov Random Field，MRF），也被称为概率无向图模型，是一种用于建模多元随机变量联合分布的统计模型，其中变量间的关系用一个无向图来表示。在这个图中，每个节点代表一个随机变量，而边则表示变量之间的潜在依赖关系。

MRF 主要用于建模那些变量间具有空间或者其他形式相互依赖性的系统，广泛应用于图像处理、空间数据分析和计算机视觉等领域。MRF 的一个关键特性是局部性原理，即给定某个变量的邻居（在图中直接与之相连的节点）后，该变量条件独立于其它所有变量。这种性质被称为马尔可夫性质。

关键概念

节点：图中的每个节点代表一个随机变量，可以是观测到的数据点或是隐藏变量。
边：节点之间的边表示变量间的直接依赖关系。
团和最大团：在图中，任何相互连接的节点集合称为团。不可能加入更多节点的团称为最大团。
势函数：用于量化节点或节点组合的概率分布，通常定义在最大团上。势函数表达了变量之间的相互作用强度。

马尔可夫性质

MRF 的核心是马尔可夫性质，即在给定一个节点的邻居的情况下，该节点与图中其他节点条件独立。这意味着，节点的局部环境提供了足够的信息来预测该节点的行为，而无需考虑更远的节点。

Hammersley-Clifford 定理

这个定理是 MRF 理论中的一个关键结果，它指出：在满足一定条件下，一个分布可以被表示为一个马尔可夫随机场，如果且仅如果它可以被表示为一个图上的势函数的乘积形式。

应用示例

在图像处理中，MRF 可以用于图像恢复、分割和纹理合成。比如，在噪声图像恢复中，每个像素点可以视为一个随机变量，相邻像素间的相关性可以用 MRF 来建模，以此推断最可能的干净图像。

求解方法

MRF 的推断和学习通常是计算密集型的，常用的方法包括吉布斯采样（Gibbs Sampling）、模拟退火（Simulated Annealing）和置信传播（Belief Propagation）等。这些方法旨在通过迭代过程来近似地估计或优化目标函数，从而解决相关的最优化问题。

Belief Propagation信念传播算法详解
马尔科夫随机场提供了一种建模多变量依赖关系的框架，而信念传播算法则是一种在这种框架下进行有效推理的方法。通过在马尔科夫随机场上运用信念传播算法，可以进行高效的概率推断和决策。

关于马尔可夫模型的问答

基础理解

请解释什么是马尔可夫链以及它的基本性质。
马尔可夫链是一种随机过程，其中下一个状态的概率仅依赖于当前状态，这被称为无记忆性。基本性质包括状态空间、初始状态概率和状态转移概率。
描述隐马尔可夫模型（HMM）及其与马尔可夫链的主要区别。
HMM是一种统计模型，它用来描述观测序列背后的一个不可见的状态序列。与马尔可夫链不同，HMM包含隐状态和观测状态，且观测状态的概率分布依赖于隐状态。
马尔可夫链的“无记忆性”或“马尔可夫性”是什么意思？请给出一个实际应用的例子。
马尔可夫性指的是系统的下一个状态仅依赖于当前状态，而与之前的历史无关。例如，天气模型中，明天是晴天还是雨天仅依赖于今天的天气，而不是之前的天气历史。
在隐马尔可夫模型中，什么是隐状态？什么是观测状态？
在HMM中，隐状态是模型中不直接可见的内部状态，而观测状态是由隐状态生成的、可以直接观察到的状态。

数学与算法

如何表示和计算马尔可夫链的状态转移概率矩阵？
状态转移概率矩阵是一个方阵，其元素 aij 表示从状态 i 转移到状态 j 的概率。（邻接矩阵）
解释隐马尔可夫模型中的前向算法和后向算法的作用。
前向算法用于计算在给定模型参数的情况下，观测序列出现的概率。后向算法也用于相似的目的，但是从序列的末尾开始计算。
什么是Viterbi算法？它在隐马尔可夫模型中用来解决什么问题？
Viterbi算法是一种动态规划算法，用于找出最有可能产生给定观测序列的隐状态序列，在HMM中用于解决解码问题。
描述Baum-Welch算法在隐马尔可夫模型中的应用及其目的。
Baum-Welch算法是一种特殊的EM算法，用于未知参数的HMM中。它通过迭代过程优化模型参数以最大化给定观测序列的概率。

应用与实践

描述一个使用隐马尔可夫模型的自然语言处理应用案例。
在自然语言处理中，HMM可用于词性标注，其中隐状态代表单词的词性，观测状态代表实际的单词。

深度与挑战

在处理非平稳时间序列数据时，马尔可夫链模型有哪些局限性，如何克服？
马尔可夫链假设转移概率不随时间变化。对于非平稳数据，可以使用时间依赖的马尔可夫模型或通过增加状态来模拟时间变化的影响。
对于有大量状态的系统，隐马尔可夫模型的性能和可行性如何？存在哪些优化或替代方案？
当状态空间很大时，HMM的计算复杂性会显著增加。可能的优化包括使用近似方法、约简状态空间或采用更高效的算法。
讨论在实际应用中构建和训练隐马尔可夫模型时可能遇到的挑战及其解决方案。
实际应用中的挑战包括数据稀疏性、参数初始化以及模型选择。解决方案可能包括使用平滑技术、合理的启发式初始化策略和交叉验证来选择模型。

【NLP】时序模型与马尔可夫模型