绪论
∑(西格玛)表示字母表,字母表中的元素称为该字母表的一个字母
ɛ 为空串,长度为 0,就是什么都没有。0 次幂代表空串
字母表的n次幂,得到的集合,其中的元素为字母表中字母构成的句子
字母表的闭包(字母表中所有字母的排列组合)
字母表的正闭包(+)加上字母表的零次幂(空串)为字母表的克林闭包(*)
注意,字母表的闭包是把字母表的 n 次幂并在一起,是各个次幂运算结果之和
字母表 ∑ 上 的语言 L,是 ∑* 的一个子集 (语言 L 是集合,满足集合运算)
L表示字母表 ∑ 上的一个语言(语言 L 就是所有句子的集合,证明语言相等,则证明集合相等),x 表示语言 L 中的一个句子,abcd表示单个字符
其关系为:a ∈ x ∈ L ⊆ ∑*
文法
V :变量,可以被其他串替换,用大写 ABC 表示
T :终极符,这个语言里边最终的句子,都是由终极符构成的串(必定含有终极符),用小写 abc 表示
P : 产生式,又叫语法规则、定义式,可以理解为一个语言的语法,字母必须要这么组合,才是该语言。A→B 读作 :A 可以定义为 / 可以为 B 。 产生式可以是终极符和非终极符构成的串,但是不能仅仅是终极符构成的串
S :开始符,即,所有推导要从该符号开始。从该符号推导出来的才是里面的句子。开始符必须是变量之一,因为只有在变量集合中才能作为产生式的左部
若产生式最终只含终极符,那么推导结束
推导:利用产生式推出新表达式,归约和其相反
G 表示文法 L(G) 表示由文法 G 定义的语言,也就是符合文法 G 的句子集合
G1 G2为两个文法 ,L(G1) = L(G2) 则,G1 G2等价,也就是句子集合相同
简化文法:只列出该文法的所有产生式,如:S→A|B|AA|BB,A→0,B→1
乔姆斯基文法体系
0型文法:最常规的文法
1型文法(上下文有关文法CSG),只需满足右边比左边长,(左边可以有终极符,可以任意长度)
2型文法(上下文无关文法CFG):在1型文法(上下文有关文法)前提下,必须满足左边是一个变量(只能有一个变量,长度为1,不能是终极符)
3型文法(正则文法RG)在2型文法的基础上,右侧为终极符串 + 一个串(注意只能有一个变量,可为空串)形如:A→w,A→wB
对应语言分别是 0,1,2,3型语言,缩写分别为:CSL,CFL,RL
正则语言 RL
线性文法
线性文法:在正则文法基础上,增加了新产生式形式:终极符串 + 一个串 + 终极符串 (注意,还是只能有一个变量)形如:A→w,A→wBx
变量代表的串在哪一侧就是哪种线性文法
右线性文法就是正则文法
左线性文法:形如:A→w,A→Bw
同一个语言用左右线性文法都可以构造,故,左线性文法与右线性文法等价
注:左线性文法 与 右线性文法 混用不是 正则文法
空语句不会改变语言类型
有穷状态自动机
有穷状态自动机(finite automata,简称 FA):识别正则语言,FA是正则语言的识别器
扩展状态转移函数:Q x *∑→ Q :一个状态读入一个字符串,变成另一个状态,*∑代表字符串
确定的有穷状态自动机(deterministic finite automata,简称 DFA)一个输入只有一个结果
构造 DFA 步骤:
- 定义 DFA 状态,每一步都干啥
- 定义转移函数,每个状态输入值后到达的新状态
- 画图,完成构造
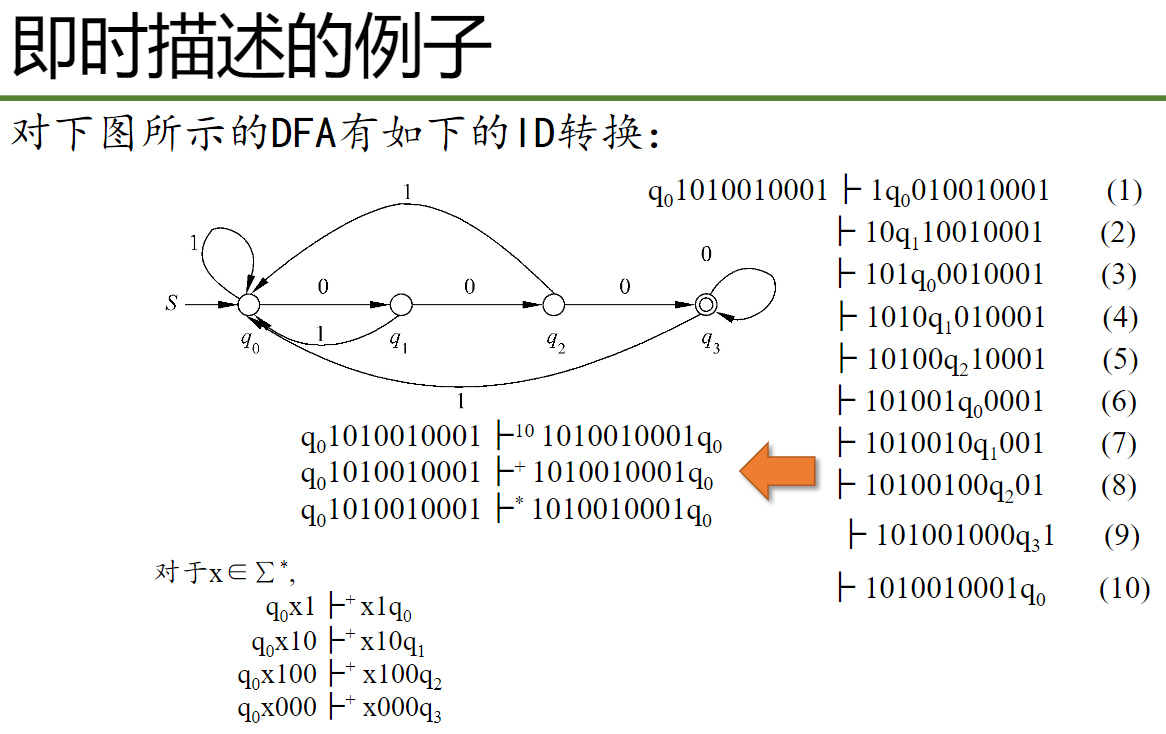
对于上面图片最下面这几行,意思是
q0x1 是即时描述的初始状态,x1q0是即时描述的终止状态,对于下面几行都一样,左边通过至少一步变为右边的终止状态,最后一个q是终止状态的符号
不确定的有穷状态自动机(Nondeterministic finite automata,简称 NFA)
输入一个字符可以转移到多个状态(多个状态是同时进行的)
NFA → DFA
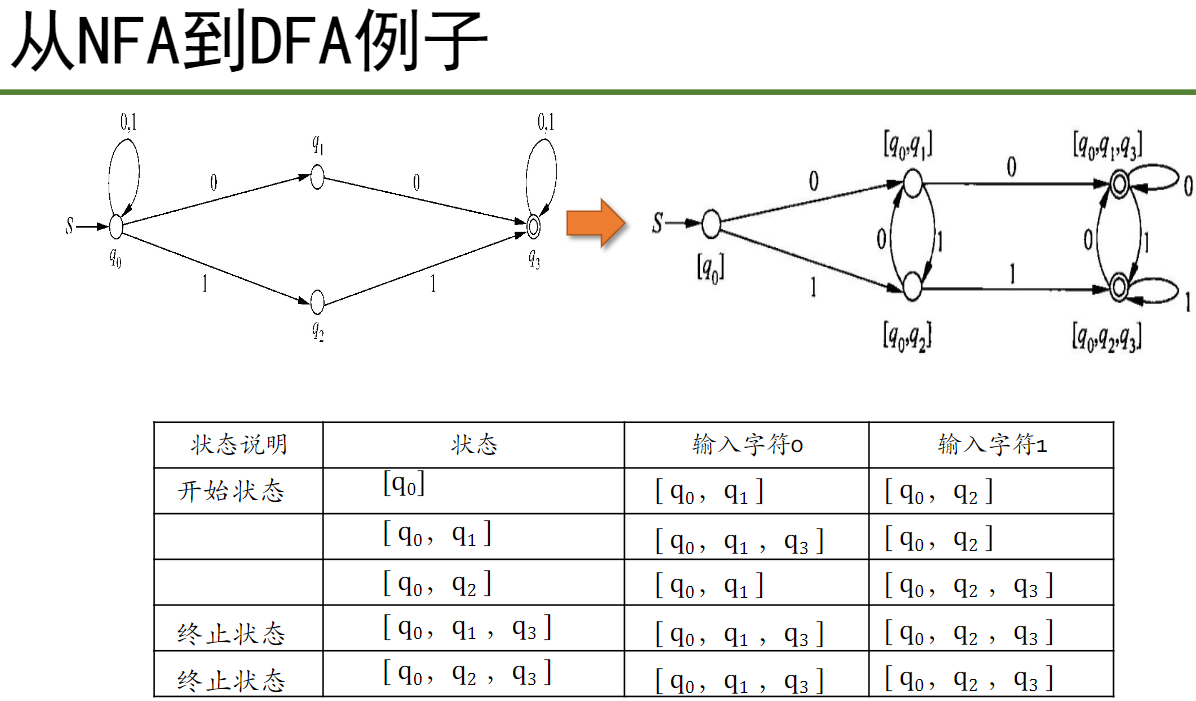
注 q3 在 NFA 中为终止状态,在新的 DFA 中含有 q3 的状态也为终止状态。同样 q0 还为起始状态。
ɛ-NFA → NFA
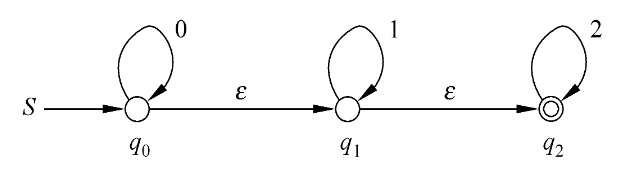

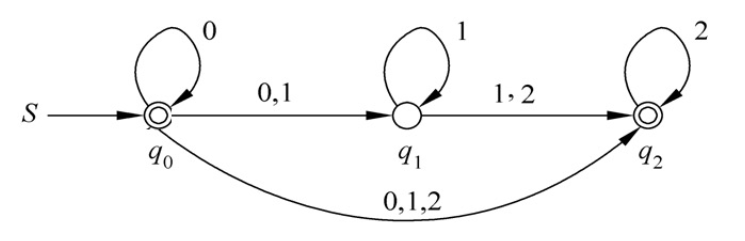
步骤
- 把 ɛ-NFA 表格列出来,准备构造 NFA 的表格。
- 画图构造 ɛ-闭包
- 当输入一个数时,把该闭包中所有能接收该数的状态的 ɛ-闭包 并集
- q0,q1,q2 还是原来的 q0,q1,q2 。
构造与 DFA 等价的正则文法 RG
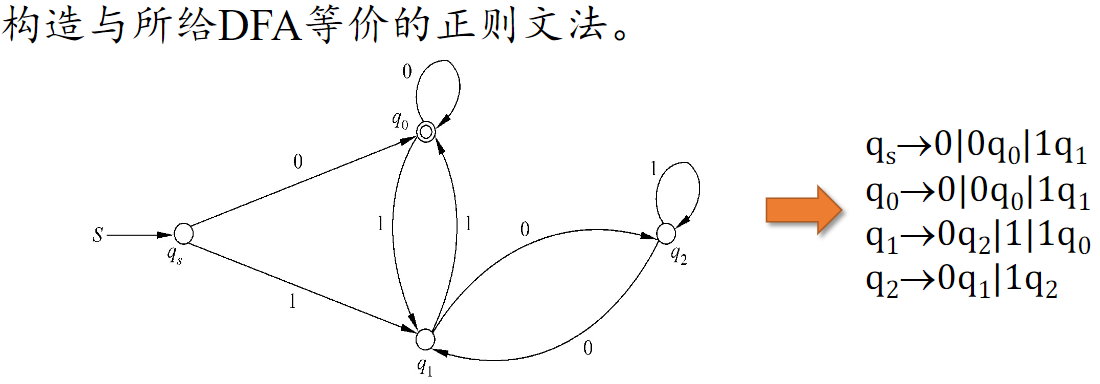
注 当某一状态 qi 是终止状态时(状态转移图表现为两个套在一起的圆),如 q0 →(0) q1,那么产生式不仅需要 q0 → 0q1,还需要 q0 → 0,因为0可能为该语的最后一位。
构造与正则文法 RG 等价的 DFA
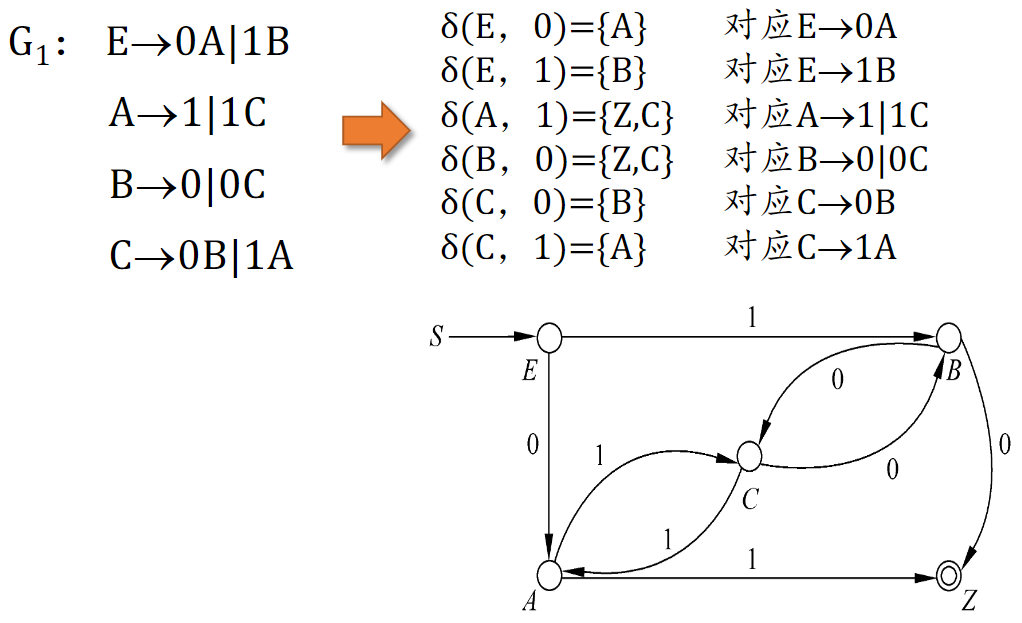
注 需要单独设置一个终止状态 Z 来接受只含终极符的转移。
左线性文法 → FA (反过来)
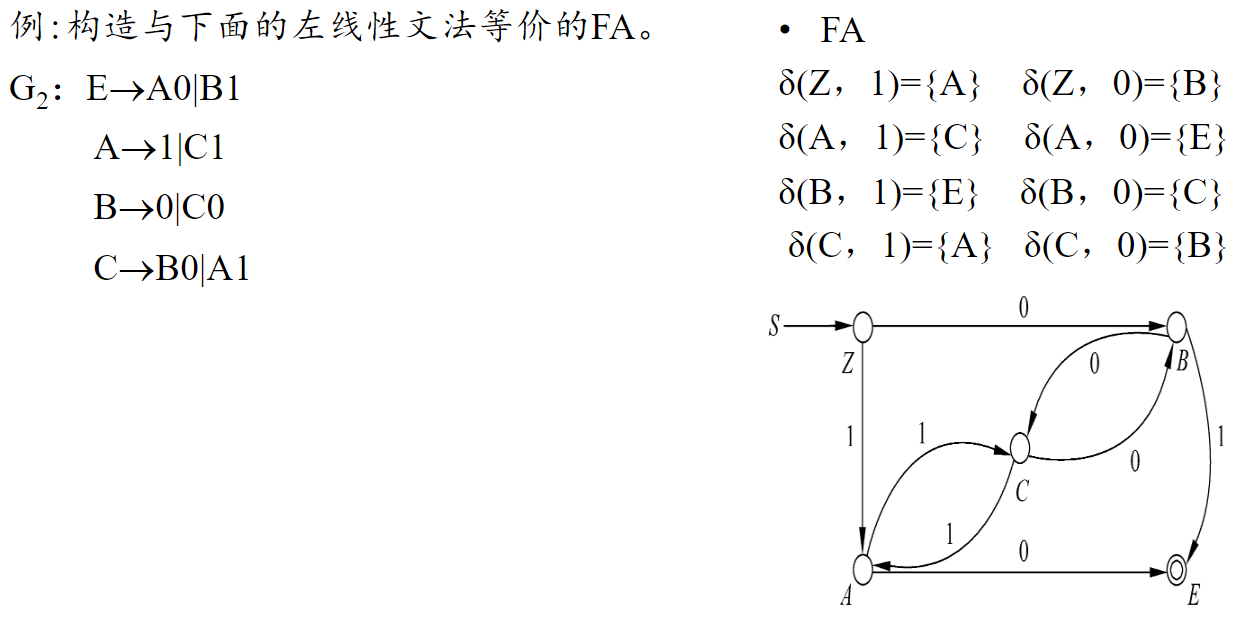
注 和正则文法完全相反,可以先按 RG → DFA 构造一遍,然后箭头全部倒置,S 的位置变为 双圆环,Z 的位置变为单元环。
FA → 左线性文法
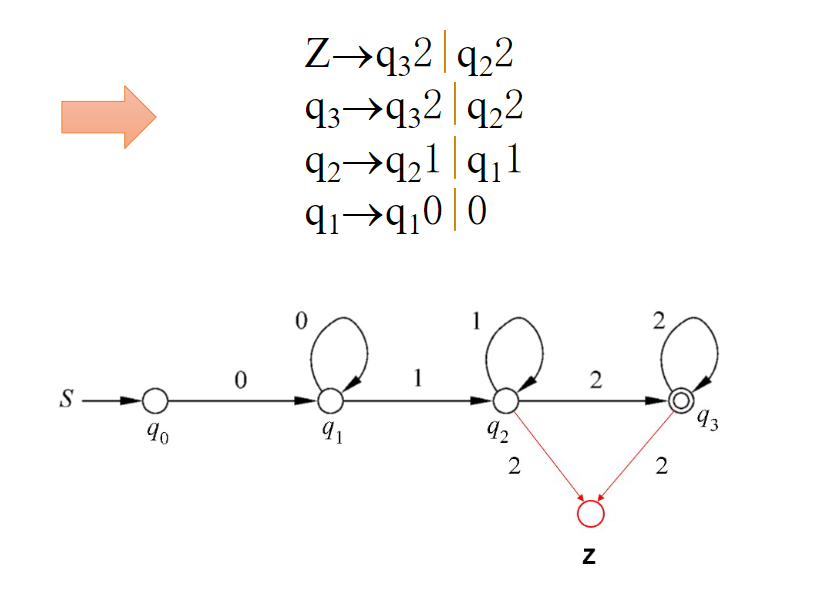
步骤
- 根据 FA 先把 RG 构造出来。
- 把单独的终极符加上一个终止状态 Z 变成 2Z。
- 全体调转,例如 q2 → 2q3 变为 q3 → q2 2
- 删除所有起始状态 q0 ,如 q1 → q0 0 变为 q1 → 0
注意:
- 起始状态前必须加 S→
- 若某一状态 qi 只有指入的箭头没有指出的箭头,则盖状态为陷阱状态,可以删除不考虑。
- 当自动机以正闭包(+)呈现时必须以空串ɛ开始,以克林闭包(*)呈现时不用。因为一个自动机必须以空串开始,而正闭包中不含空串。
- 当由 RG → FA 时,需要自己设置一个终止状态Z,用于接收A→1 | 1C 这样的产生式;相反的,左线性文法构造FA时,需要自己设置一个开始状态Z,同样,产生式箭头也和RG相反,例如,A→1 | C1 , 意思时,由开始状态Z读入1跳转到状态A,由状态C读入一个1跳转到状态A。
正则表达式
正则表达式(regular expression,RE)
形式定义:
前三条都是定义基本字符串,Ø 为空集,ɛ 为空字符串,a 为任意字符。
第四条说的是前三条的元素根据第四条的运算可以形成正则表达式。
第一种运算 (r+s) 是集合的并集。
第二种运算 (rs) 是指 r 和 s 串的连接
第三种是克林闭包,(r*) = ( r0+r1+r2+….. )
注 正则表达式必须加括号
正则表达式RE r ,记作L(r),也是一种语言,是一个集合,也可直接记作r
注:Ø的零次幂是 ɛ
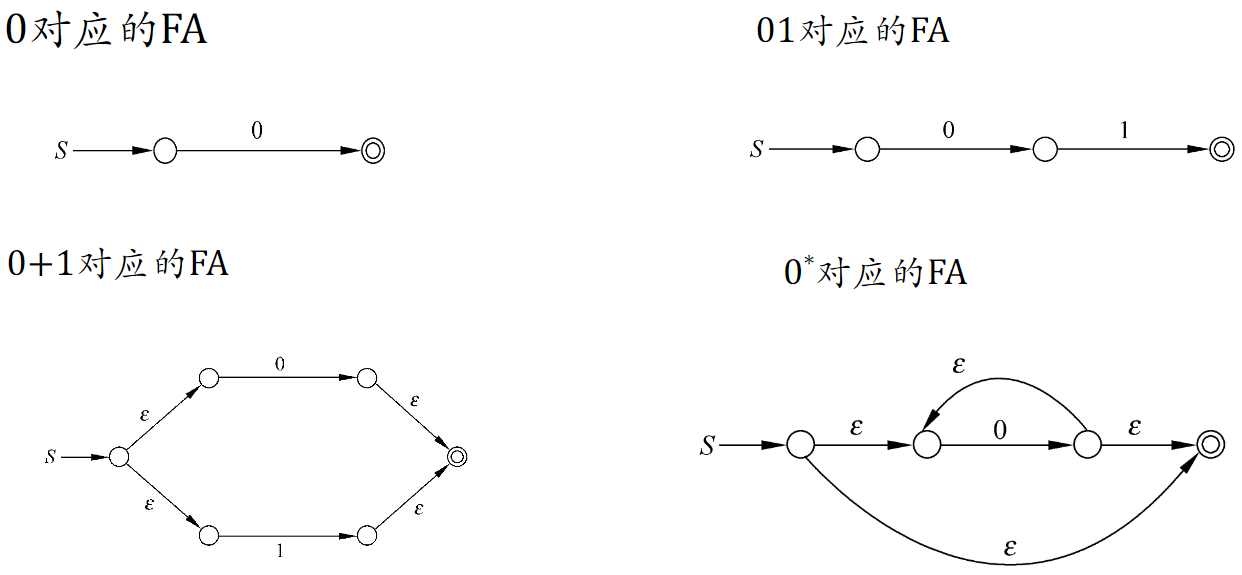
RE → FA
记住下面几个基本元素,拼接即可
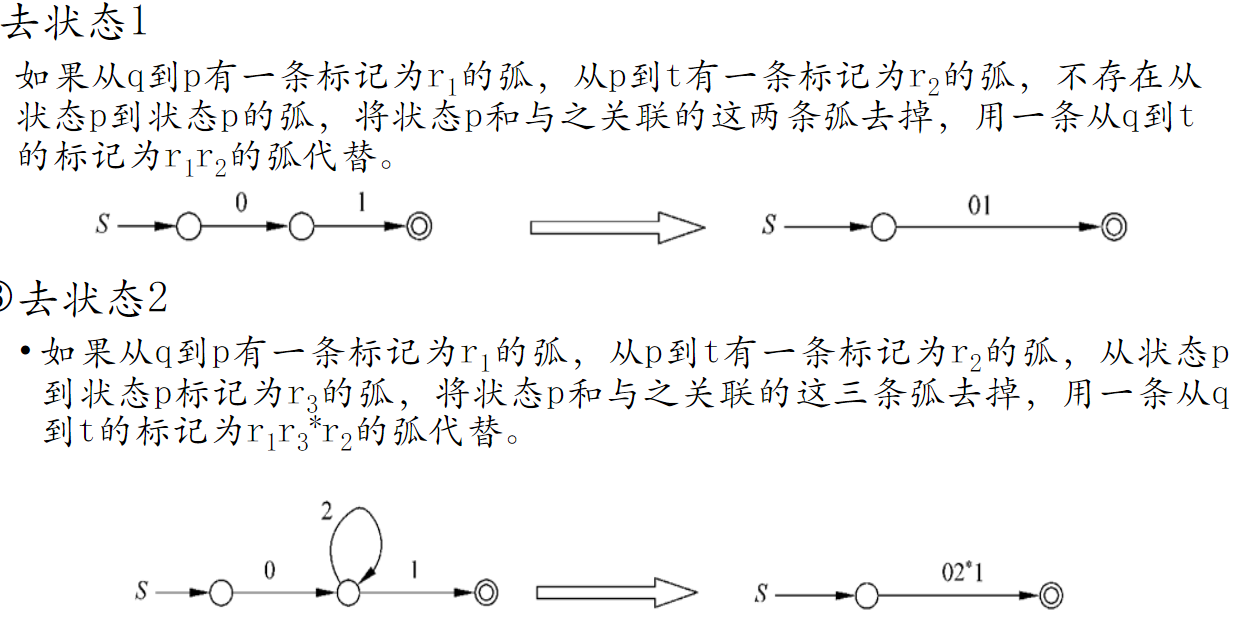
正则语言 RL / DFA → RE
- 先增加两个状态,一个起始状态 X 一个终止状态 Y ,为了终止状态唯一
- 选取一个状态分析(最好是终止状态前一个状态,因为好分析),找出该状态的出度入度,分析是闭包运算,还是并集运算还是连接运算。然后用正则表达式替换
注并弧用加号
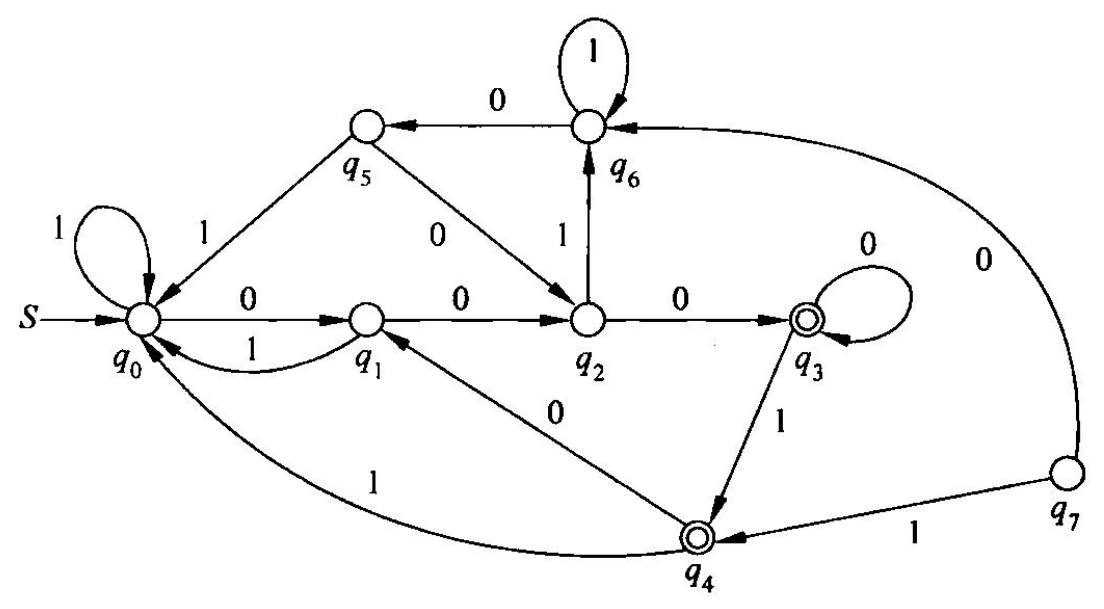
正则语言的性质
如果一个语言是正则语言,那么一定满足泵引理,反之不成立。
正则语言的封闭性:经过运算还为正则语言
DFA 极小化
步骤
- 构造表格,如果有不可达状态则先删除,左边列是 1~n 下面行是 0~n-1
- 所有终点为一组,行列标上 x
- 任意找两个其他未标注的点,看两个点到终点的路径,分别看输入一个数,输入两个数,输入三个数后,是否相同,只要存在相同的路径,则两个点为不可区分,不用标注;无论怎么都找不到,则为可区分,标上 x。注意,不能走自环,只能走直路。

上下文无关语言
上下文无关文法:CFG
派生树: 一定是上下文无关文法 CFG 的派生树。
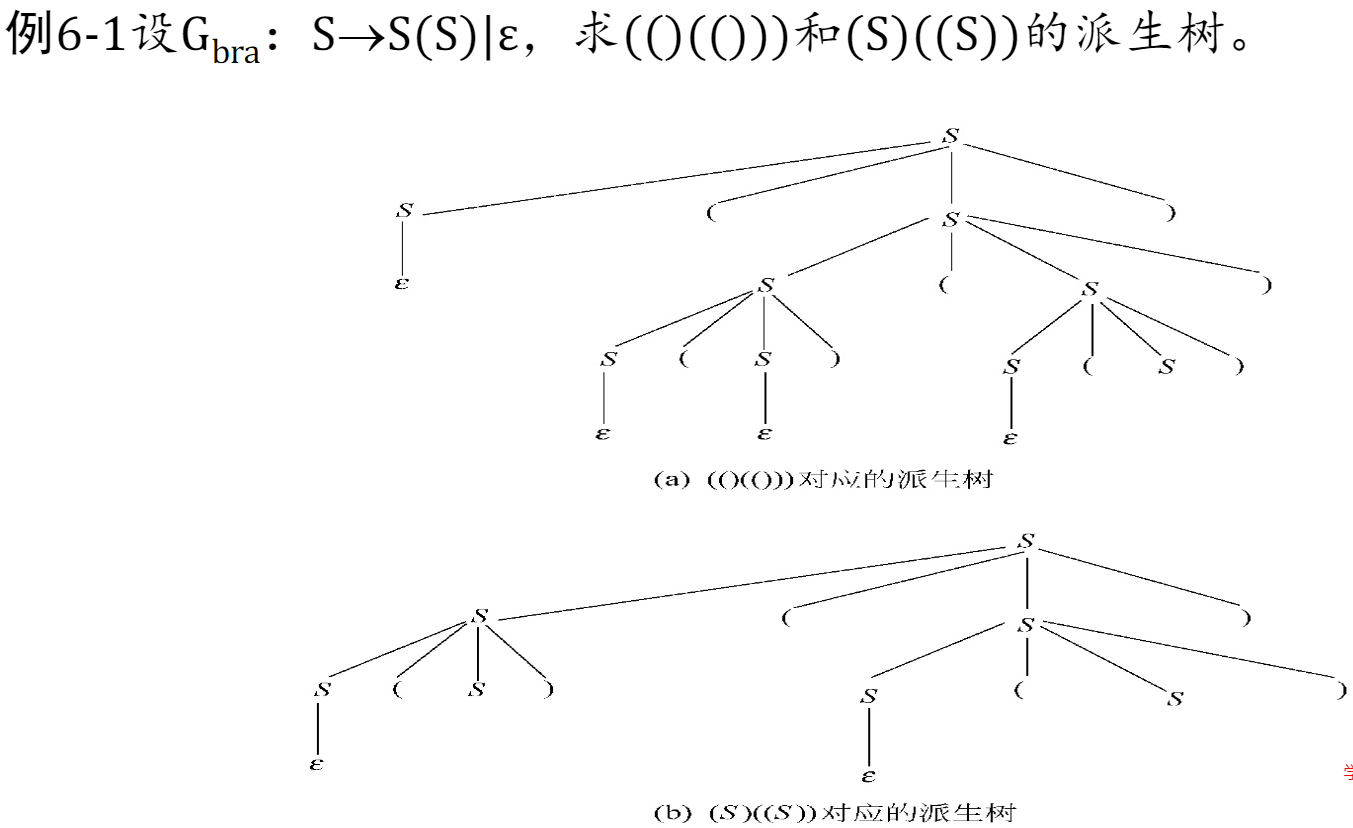
最左派生:从最左边开始替换,最右、随机同理。
派生树越靠近叶子节点(越在下面),优先级越高。
随机派生有多少种方式,就有多少种派生。计算派生时,找到派生树种所有的变量(ABC),计算所有变量的排列数,即为派生数。但是要注意固有顺序不能变。
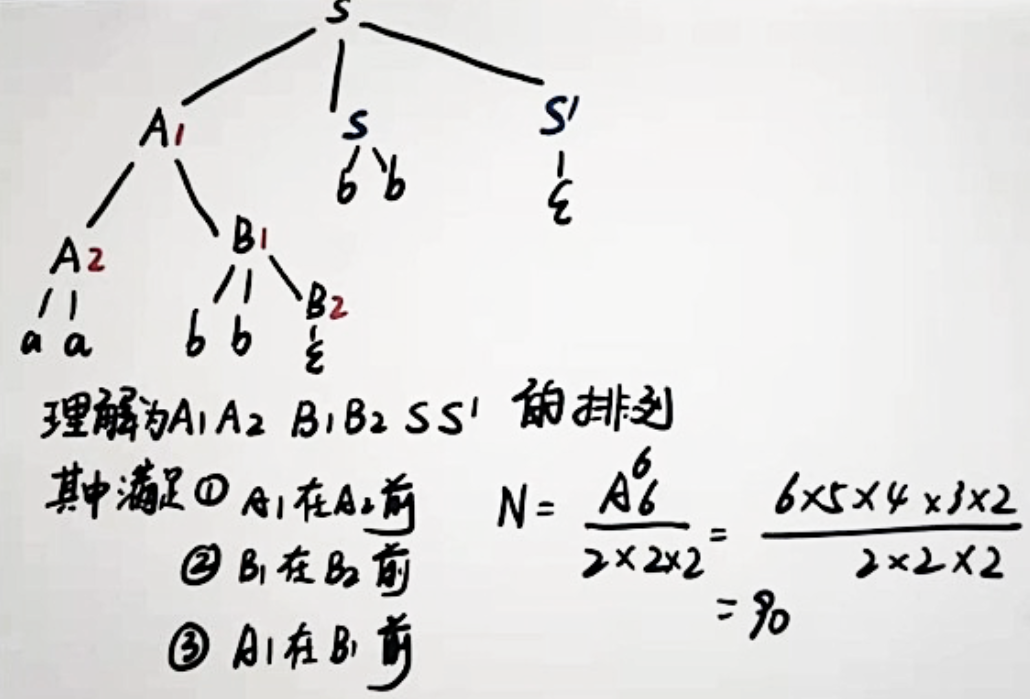
根据派生树写出原 CFG 直接看图就行。

CFG 的化简
步骤
- 删除无用符号(注意要把不可达状态的整个表达式都删了,比如 S→AB,B 不存在,则 AB 都删)
- 删除 ɛ 产生式
- 删除单一产生式(形如 A → B)
- 再次出现无用符号时,再次删除无用符号
例
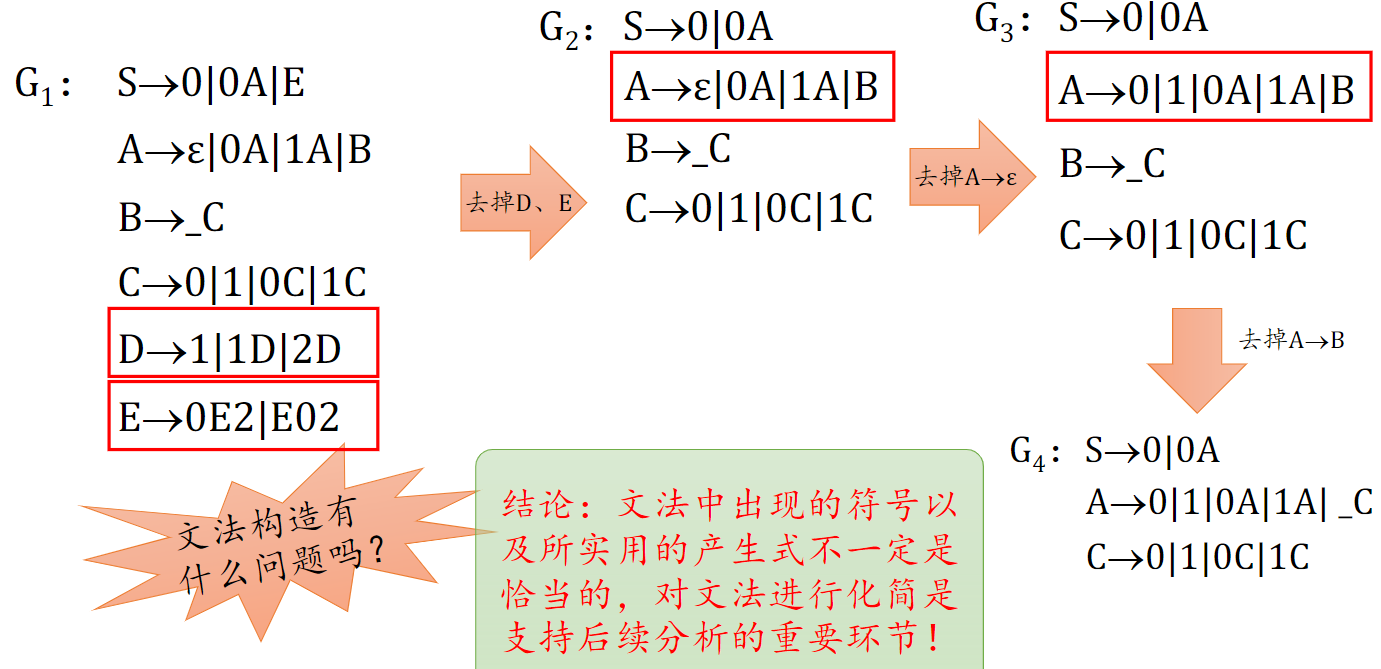
去除 ɛ 产生式的例子

任何不含空串的CFG都能转化为 CNF / GNF
乔姆斯基范式: CNF,形如 A → BC 、 A → a,在化为 CNF 前需先简化

格雷巴赫范式: GNF,形如 A → a 、 A → aBCDE.... ,在化为 GNF 前需先简化
需要消除左递归(把左递归变为右递归),形如:A → Aβ

简例
A → A0 | 1
变为:
A → 1
A → 1B
B → 0B
B → 0

下推自动机 PDA
PDA 是 ɛ-NFA 增加了一个栈
PDA 用于识别一个·句子是否满足上下文无关文法(识别上下文无关语言)
PDA 的构成:
M = (Q ,∑,Γ,δ,q0,Z0,F)
Q :状态的集合 {q0 q1 q2}
∑:输入字母表,要识别的句子含有的符号,如{a,b,c} {1,2,3}
Γ:栈符号表,对应 CFG 中的变量 {S,A,B,C}
δ:状态转移函数,有两种格式,在下面给出
q0:起始状态
Z0:开始符号,开始时栈底的元素
F:终止状态集合{q1 q2 q3},空栈接受时 F 为 Ø
状态转移函数 δ 的两种格式
常规转移
δ(q,a,Z)={(p1,γ1)0(p2,γ2),...,(pm,γm)}
表示状态 q 时,读入句子中的符号 a ,弹出栈顶符号 Z ,转移到新状态 pi ,将 γi 中的符号从右向左压入栈。
例1
δ1(q0,1,S)={(q0,SB)}
在状态 q0 时,读入 1 ,弹出栈顶元素 S ,转移到新状态 q0 ,将 SB 串以 B、S 的顺序入栈(B 在 S 的下面)
例2
δ1(q0,0,A)={(q0,ε)}
在状态 q0 时,读入 0 ,弹出栈顶元素 A ,转移到新状态 q0 ,将 ε 入栈
ɛ 转移
δ(q,ɛ,Z)={(p1,γ1)0(p2,γ2),...,(pm,γm)}
表示状态 q 时,读入句子中的符号 a ,弹出栈顶符号 Z ,转移到新状态 pi ,将 γi 中的符号从右向左压入栈。
例
δ2(q0,ε,Z)={(q1,ε)}
在状态 q0 时,读入 1 ,弹出栈顶元素 S ,转移到新状态 q0 ,将 SB 串以 B、S 的顺序入栈(B 在 S 的下面)
构造 PDA
CFG → PDA
空栈接受
- 化为 CFG
- CFG → GNF
- 写出 GNF 的最左派生,注明 PDA 转移函数要做的动作
- 写出 PDA

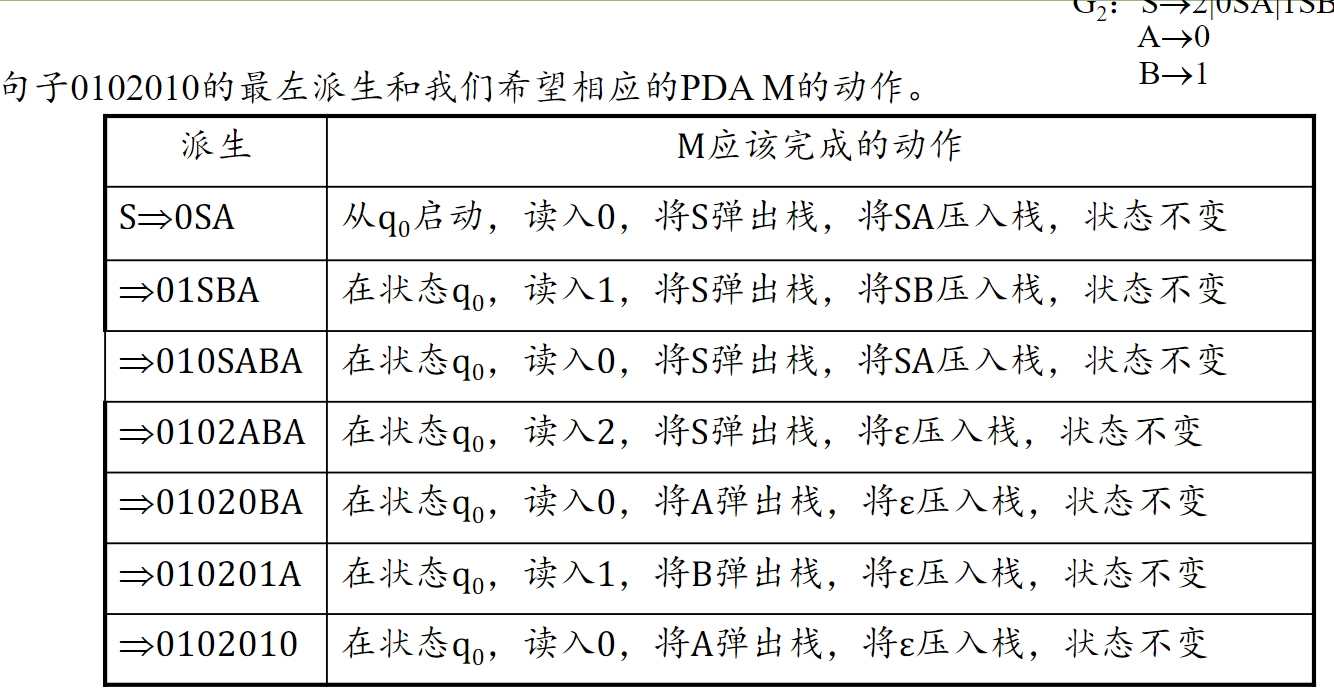

终态接受
和空栈接受对比:
-
符号的添加:
添加一个开始符号 Z0、一个栈底符号 Z 、一个终止状态 q1
从 Z0 开始,弹出 Z0,把 Z 压入栈底,当栈内只剩 Z 时,跳转到 q1 终止状态 -
转移函数的添加:
原状态转移函数都不变,找到原栈底元素的转移函数,这里是含有 S 的三个转移函数,把 S 改为新定义的栈底符号 Z0,在右边入栈中加上新的栈底元素 Z 。对于右边是 ε 的转移,只改动 Z0,ε 不变。
此外,还需在最后添加遇到 Z 转移到 q1 的转移函数。

空栈接受的 PDA → 终态接受的 PDA (二者等价)
CFG → 空栈接受的 PDA
图灵机 TM
M=(Q, ∑, Γ, δ,q0 , B, F)
Q :状态的集合 {q0 q1 q2}
∑:输入字母表,要识别的句子含有的符号,如{a,b,c} {1,2,3}
Γ:带符号表,对应 CFG 中的变量 {S,A,B,C}
δ:状态转移函数,有两种格式,在下面给出
q0:起始状态
B:空白符
F:终止状态集合{q1 q2 q3}
状态转移函数 δ 的两种格式
右移
δ(q,X)=(p,Y,R)
表示状态 q 时,读入句子中的符号 X ,弹出栈顶符号 Z ,将状态改为 p ,并在 X 所在的带方格中印刷符号 Y,然后将读头右移一格
左移
δ(q,X)=(p,Y,L)
表示状态 q 时,读入句子中的符号 X ,弹出栈顶符号 Z ,将状态改为 p ,并在 X 所在的带方格中印刷符号 Y,然后将读头左移一格
图灵机接受的语言
若可接受:停机+接受
若不可接受:停机+拒绝 / 永不停机

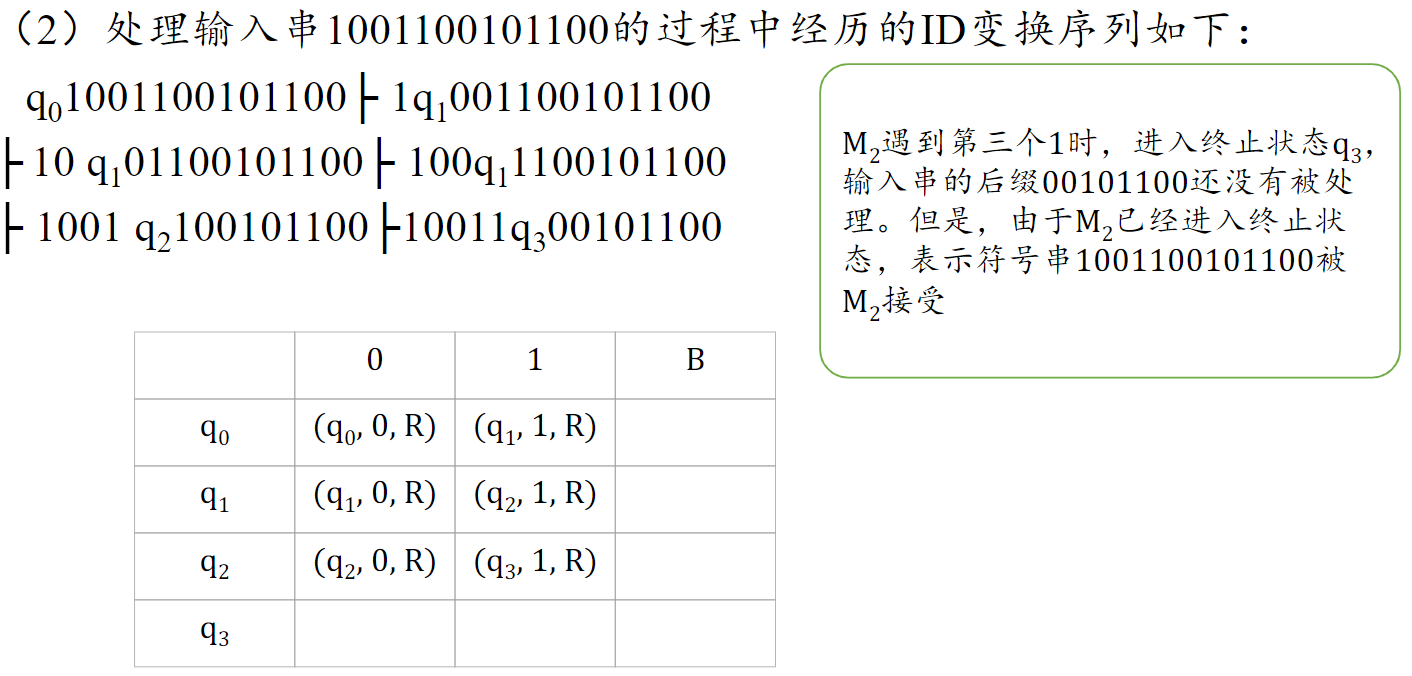

构造图灵机
- 把要识别的句子模拟写在纸带上
- 逐渐向右移动,观察能否用替换(标记)等方式识别走过的路
- 设置好不同的状态,不同的输入,列出表格

